Difference between revisions of "Sigma"
(→1 SIGMA) |
(→2 SIGMA) |
||
| Line 21: | Line 21: | ||
If someone says that an error is 1 sigma, then that person is referring to the greatest possible error in between the lines marked with - 1 sigma to + 1 sigma in the bell curve (see the curve above). Add the percentages of the two regions under the bell to get about 68%. There is a 68% chance that the error will not exceed the value stated. | If someone says that an error is 1 sigma, then that person is referring to the greatest possible error in between the lines marked with - 1 sigma to + 1 sigma in the bell curve (see the curve above). Add the percentages of the two regions under the bell to get about 68%. There is a 68% chance that the error will not exceed the value stated. | ||
| − | === 2 SIGMA === | + | === 2 SIGMA - 95% Chance === |
| − | If someone says that an error is 2 sigma, then that person is referring to the greatest possible error in between the lines marked with - 2 sigma to + 2 sigma in the bell curve (see the curve above). Add the percentages of the | + | If someone says that an error is 2 sigma, then that person is referring to the greatest possible error in between the lines marked with -2 sigma to +2 sigma in the bell curve (see the curve above). Add the percentages of the four regions under the bell between the - and + sigma lines to get about 95%. There is a 95% chance that the error will not exceed the value stated. |
| + | |||
| + | === 3 SIGMA - 95% Chance === | ||
| + | |||
| + | If someone says that an error is 3 sigma, then that person is referring to the greatest possible error in between the lines marked with -3 sigma to +3 sigma in the bell curve (see the curve above). Add the percentages of the six regions under the bell to get about 95%. There is a 95% chance that the error will not exceed the value stated. | ||
Revision as of 23:57, 3 October 2011
|
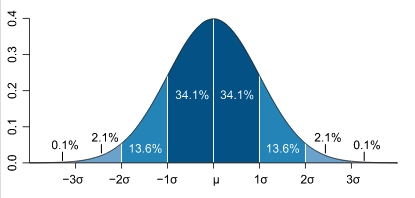
Most have heard of the "bell curve" in mathematics. This is the shape that describes the probability that a given percentage of measurements will fall within a certain region under a standard bell curve. This shape is found in nature - so its one that mathematicians use often. This shape of the standard bell curve is called "Normal Distribution" or "Gausian Distribution." |
Contents |
HOW SIGMA PERTAINS to the BELL CURVE
A statistical measurement called "standard deviation" is also referred to as "sigma" on the horizontal axis of a bell curve. Basically, this is a measurement of how much the measurements vary from the center value by a distance of a value called "sigma" on either side of the center of the curve.
1 SIGMA
If someone says that an error is 1 sigma, then that person is referring to the greatest possible error in between the lines marked with - 1 sigma to + 1 sigma in the bell curve (see the curve above). Add the percentages of the two regions under the bell to get about 68%. There is a 68% chance that the error will not exceed the value stated.
2 SIGMA - 95% Chance
If someone says that an error is 2 sigma, then that person is referring to the greatest possible error in between the lines marked with -2 sigma to +2 sigma in the bell curve (see the curve above). Add the percentages of the four regions under the bell between the - and + sigma lines to get about 95%. There is a 95% chance that the error will not exceed the value stated.
3 SIGMA - 95% Chance
If someone says that an error is 3 sigma, then that person is referring to the greatest possible error in between the lines marked with -3 sigma to +3 sigma in the bell curve (see the curve above). Add the percentages of the six regions under the bell to get about 95%. There is a 95% chance that the error will not exceed the value stated.
Now three sigma is 3* the standard deviation, which statistically mean that 99.73% of the time a measurement is made it will be within 3*the standard deviation of the actual value. It is thus a way to compare how good the measurement method is.
In similar ways 2 sigma means within 95% of the actual value and 6 sigma means as close to always as is resonable to ever need.