Difference between revisions of "Sigma"
(→HOW SIGMA PERTAINS to the BELL CURVE) |
(→HOW SIGMA PERTAINS to the BELL CURVE) |
||
| Line 32: | Line 32: | ||
===HOW SIGMA PERTAINS to the BELL CURVE=== | ===HOW SIGMA PERTAINS to the BELL CURVE=== | ||
| − | A statistical measurement called "standard deviation" is also referred to as the region between the two sigma lines on the horizontal axis of a bell curve. The region between the two lines under the bell are is the region called "1 sigma". The lower case Greek letter sigma is used like this: [[image:plus_1_sigma.jpg|250px]] This is a probability of how much the measurements vary from the center value of the bell by a distance defined as sigma on either side of that center. (See + and - sigma in the graph above.) | + | A statistical measurement called "standard deviation" is also referred to as the region between the two sigma lines on the horizontal axis of a bell curve. The region between the two lines under the bell are is the region called "1 sigma". The lower case Greek letter sigma is used like this: [[image:sigma.jpg|250px]] The sigma symbol is combined with numbers like this to help us know how many sigma regions we are referring to: [[image:plus_1_sigma.jpg|250px]] This is a probability of how much the measurements vary from the center value of the bell by a distance defined as sigma on either side of that center. (See + and - sigma in the graph above.) |
=== 1 SIGMA - 68% Chance === | === 1 SIGMA - 68% Chance === | ||
Revision as of 00:24, 4 October 2011
|
SIGMA and ERRORSBack to VTube-LASER |
|
Contents |
|
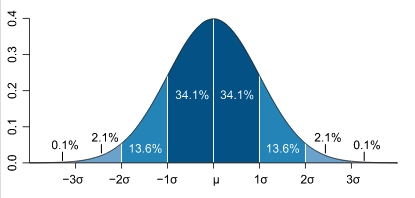
Most have heard of the "bell curve" in mathematics. This is the shape that describes the probability that a given percentage of measurements will fall within a certain region under a standard bell curve. This shape is found in nature - so its one that mathematicians use often. This shape of the standard bell curve is called "Normal Distribution" or "Gausian Distribution." |
|
HOW SIGMA PERTAINS to the BELL CURVE
A statistical measurement called "standard deviation" is also referred to as the region between the two sigma lines on the horizontal axis of a bell curve. The region between the two lines under the bell are is the region called "1 sigma". The lower case Greek letter sigma is used like this: 
The sigma symbol is combined with numbers like this to help us know how many sigma regions we are referring to: 
This is a probability of how much the measurements vary from the center value of the bell by a distance defined as sigma on either side of that center. (See + and - sigma in the graph above.)
1 SIGMA - 68% Chance
If someone says that an error is 1 sigma, then that person is referring to the greatest possible error in between the lines marked with - 1 sigma to + 1 sigma in the bell curve (see the curve above). Add the percentages of the two regions under the bell to get about 68%. There is a 68% chance that the error will not exceed the value stated.
2 SIGMA - 95% Chance
If someone says that an error is 2 sigma, then that person is referring to the greatest possible error in between the lines marked with -2 sigma to +2 sigma in the bell curve (see the curve above). Add the percentages of the four regions under the bell between the - and + sigma lines to get about 95%. There is a 95% chance that the error will not exceed the value stated.
3 SIGMA - 99.6% Chance
If someone says that an error is 3 sigma, then that person is referring to the greatest possible error in between the lines marked with -3 sigma to +3 sigma in the bell curve (see the curve above). Add the percentages of the six regions under the bell to get over 99%. There is a 99.6% chance that the error will not exceed the value stated.
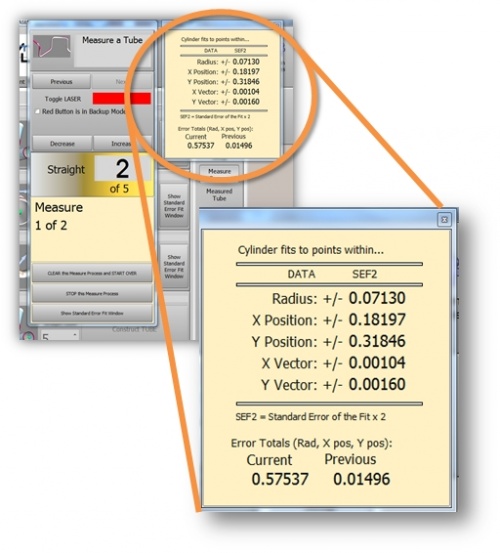
2 SIGMA and VTube-LASER SEF2 Values
The 2 Sigma value is used quite a bit for measuring. For example, when VTube-LASER reports Cylinder Fit errors, it always shows the values as "SEF2" or "standard error fit X 2" - which is the same as 2 sigma or (2 times the sigma) value calculated. This lets you know there is a 95% chance that the error or deviation reported in the Cylinder Fit window will not exceed that value.
