Difference between revisions of "Sigma"
m (→How does SIGMA Apply to a Standard Bell Curve?) |
|||
| Line 54: | Line 54: | ||
=== "1 SIGMA" = 68% Chance ([[image:fromto1sigma.jpg|150px]]) === | === "1 SIGMA" = 68% Chance ([[image:fromto1sigma.jpg|150px]]) === | ||
| − | + | For predicting the greatest error in a measuring center, if someone says that an an error value is repeatable within 1 sigma, then that person is referring to the greatest possible error in between the lines marked with - 1 sigma to + 1 sigma in the bell curve. Add the percentages of the two regions under the bell to get about 68%. There is a 68% chance that the error will not exceed the value stated. | |
=== "2 SIGMA" = 95% Chance ([[image:fromto2sigma.jpg|150px]])=== | === "2 SIGMA" = 95% Chance ([[image:fromto2sigma.jpg|150px]])=== | ||
Revision as of 00:40, 4 October 2011
SIGMA and ERRORSBack to VTube-LASER |
Contents |
|
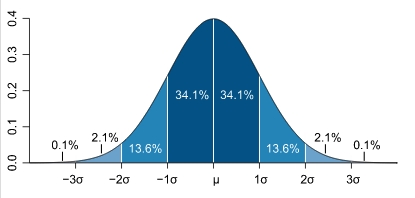
Most have heard of the "bell curve" in mathematics. This is the shape that describes the probability that a given percentage of measurements will fall within a certain region under a standard bell curve. This shape is found in nature - so its one that mathematicians use often to predict the chance that something will occur in nature. This shape of the standard bell curve is called "Normal Distribution" or "Gausian Distribution." |
How does SIGMA Apply to a Standard Bell Curve?
|
A statistical measurement called "standard deviation" is also referred to as the region between the two sigma lines on the horizontal axis of a bell curve. The region between the two lines under the bell is the region called "1 sigma". The lower case Greek letter sigma is used like this: |
|
|
The sigma symbol is combined with numbers like this to help us know how many sigma regions we are referring to in the bell curve. |
"1 SIGMA" = 68% Chance (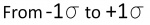 )
)
For predicting the greatest error in a measuring center, if someone says that an an error value is repeatable within 1 sigma, then that person is referring to the greatest possible error in between the lines marked with - 1 sigma to + 1 sigma in the bell curve. Add the percentages of the two regions under the bell to get about 68%. There is a 68% chance that the error will not exceed the value stated.
"2 SIGMA" = 95% Chance (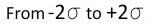 )
)
If someone says that an error is 2 sigma, then that person is referring to the greatest possible error in between the lines marked with -2 sigma to +2 sigma in the bell curve (see the curve above). Add the percentages of the four regions under the bell between the - and + sigma lines to get about 95%. There is a 95% chance that the error will not exceed the value stated.
"3 SIGMA" = 99.6% Chance (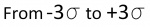 )
)
If someone says that an error is 3 sigma, then that person is referring to the greatest possible error in between the lines marked with -3 sigma to +3 sigma in the bell curve (see the curve above). Add the percentages of the six regions under the bell to get over 99%. There is a 99.6% chance that the error will not exceed the value stated.
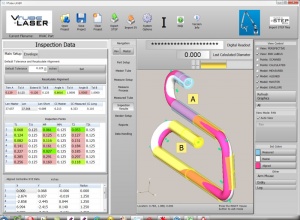
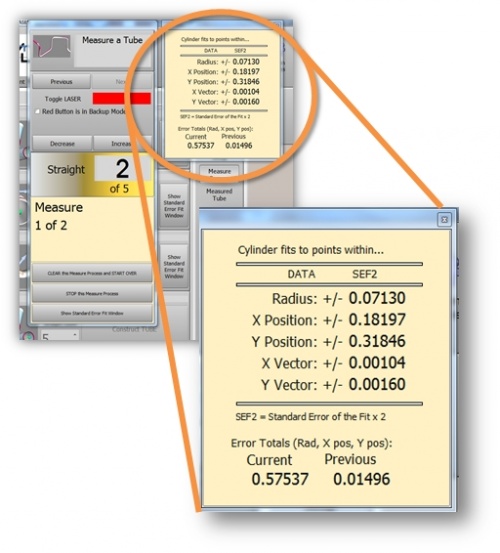
How "2 SIGMA" applies to VTube-LASER SEF2 Values
The 2 Sigma value is used quite a bit for measuring. For example, when VTube-LASER reports Cylinder Fit errors, it always shows the values as "SEF2" or "standard error fit X 2" - which is the same as 2 sigma or (2 times the sigma) value calculated. This lets you know there is a 95% chance that the error or deviation reported in the Cylinder Fit window will not exceed that value.
Other Pages
Back to VTube-LASER
Back to VTube-STEP